xgboost之分位点算法 2017.09.11

1. 基本概念

1.1 分位点

输入数据： 14, 19, 3, 15, 4, 6, 1, 13, 13, 7, 11, 8, 4, 5, 15, 2

则排序后，该组数据为： 1, 2, 3, 4, 4, 5, 6, 7, 8, 11, 13, 13, 14, 15, 15, 19. 如下图所示：

在上面的序列中，

• 第1小的数是什么？ 很明显是：1 ($rank=1$)
• 第4小的数是什么？ 答案是：4 ($rank=4$)
• 第50%小的数是什么？ 50% * 16 = 8（$rank=8$)， 则答案为：7

什么是分位点呢？ ϕ-quantile表示 $rank = \lfloor ϕ-quantile \times N \rfloor$的元素，其中，$N$为序列中元素的个数。例如，在上面的例子中：

• 0.25-quantile是什么？ $rank=0.25 \times 16=4$，所以答案为：4
• 0.5-quantile是什么？ $rank=0.5 \times 16=8$，所以答案为：7

1.2 ε-approximate 分位点

假定序列的大小为$N$，给定误差$\varepsilon$和$rank=r$，其$\varepsilon-approximate$ 分位点为序列中的一些元素，且这些元素的rank值$r^\prime$满足：$r^ \prime \in [r-\varepsilon N, r+\varepsilon N]$。以上面的序列为例，给定$\varepsilon=0.1, ϕ=0.5$，此时$r=0.5 \times 16=8$，则rank值在区间$[6.2, 9.6]$的元素为：$\{6, 7, 8\}$，即： *0.1-appoximate 0.5-quantile*为：$\{6, 7, 8\}$

注意：ϕ-quantile对应区间的计算方法在参考[3]和参考[4]有所不同（是否取整，如何取整），这里采用参考[3]中的方法

1.3 quantile summary

ε-approximate quantile summary 是一种数据结构，该数据结构能够以 $\varepsilon N$的精度计算任意的分位查询。当一个序列无法全部加载到内存时，常常采用quantile suammary近似的计算分位点。

An ε-approximate quantile summary of a sequence of N elements is a data structure that can answer quantile queries about the sequence to within a precision of εN [5].

下图展示了上面序列的一个quantile suammary，可以看出：quantile summary中value是原序列的一个子集，通过这种方式就能达到减少数据量的效果。

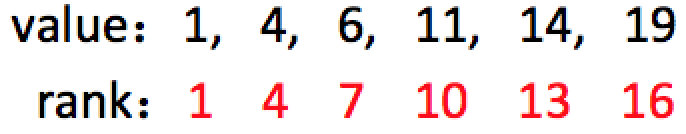
如何利用quantile summary呢？

第2小的数是什么？ 在上面的quantile summary中，与2最近的rank为1，则答案近似为：1 ($rank=1$) 第25%小的数是什么？ ($0.25 % 16=4$)，在上面的quantile summary中，与4最近的rank为4，则答案“近似”为：4($rank=4$)

注意：在quantile summary中，需要保留原序列中的最小值和最大值。

2. 加权分位点

在上面的描述中，每个数据的计数都为1，即权重都为1，所以rank的取值也都是整数。在xgboost中，每个样本的权重会出现小数，此时会出现这这样的情况：“第0.5个元素是什么？”。如下图所示，第0.5个元素为：3。

当数据量非常大时，也需要使用quantile summary的方式来近似计算分位点。

在xgboost中，需要根据特征值以及样本的权重分布，近似计算特征值的分位点，实现近似分割算法。近似计算特征值分位点的算法称为：weighted quantile sketch[2]，该算法满足quantile summary通常的两个操作：merge和prune。

2.1 定义和结论

2.1.1 基本定义

给定multi-set $D=\{(x_1, w_1), (x_2, w_2), \cdots (x_n, w_n)\}$，其中：$x_i \in R, w_i \in [0, +\infty]$，假定顺序为：升序。定义两个排序函数$r_D^-(y), r_D^+(y): R \to [0, +\infty]$,

$r_D^-(y)=\sum_{(x_i, w_i) \in D, w_i < y}w$ $r_D^+(y)=\sum_{(x_i, w_i) \in D, w_i \le y}w$

这两个函数对应上面的rank取值，分别表示特征值$y$ rank取值的最小值和最大值，这里需要注意函数的定义域。

由于D是multi-set，所以可能存在完全相同的 $(x, w)$。

定义权重函数：

$$w(y)=r_D^+(y) - r_D^-(y) = \sum_{(x_i, w_i) \in D, x_i=y}w$$

整个数据集上的权重和定义为：

$$w(D)=\sum_{(x_i, w_i) \in D}w$$

2.1.2 quantile summary of weighted data

加权数据的quantile suammary定义为四元组：

$$Q(D) = (S, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$$

其中: $S=\{x_1, x_2, \cdots, x_k\}, x_i \in \{x\|(x, w) \in D\}$,

满足以下条件：

1. 对于所有的$i$，满足$x_{i} < x_{i+1}$，且$x_1, x_k$分别是最小值和最大值，即：$x_1=min_{(x, w)\in D}x, x_k=max_{(x, w)\in D}x$
2. $\tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D}$ 三个函数:$S \to [0, +\infty]$，并且有：1） $\tilde{r}^{-}_{D}(x_i) \le r^{-}_{D}(x_i)$； 2） $\tilde{r}^{+}_{D}(x_i) \ge r^{+}_{D}(x_i)$；3） $\tilde{w}_{D}(x_i) \le w_{D}(x_i)$。当$i \in \{1, k\}$时，取得等号
3. $\tilde{r}^{-}_{D}(x_i) + \tilde{w}_{D}(x_i) \le \tilde{r}^{-}_{D}(x_{i+1})$，并且：$\tilde{r}^{+}_{D}(x_i) \le \tilde{r}^{+}_{D}(x_{i+1}) - \tilde{w}_{D}(x_{i+1})$

提示： $x_{i} < x_{i+1}$，严格递增，$x_{i}$和$x_{i+1}$之间可能包含很多元素，但这些元素并不在summary中（所以才有第3条特性）

2.1.3 函数定义域扩展

函数$\tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D}$的定义域为$S$，现将其扩展到实数域。

当$y<x_{1}$时，$\tilde{r}^{-}_{D}(y)=0, \quad \tilde{r}^{+}_{D}(y)=0, \quad \tilde{w}_{D}(y)=0$

当$y>x_{k}$时，$\tilde{r}^{-}_{D}(y)=\tilde{r}_D^{+}{x_{k}}, \quad \tilde{r}^{+}_{D}(y)=\tilde{r}_D^{+}{x_{k}}, \quad \tilde{w}_{D}(y)=0$

当$y \in [x_{i}, x_{i+1}]$时，$\tilde{r}^{-}_{D}(y)=\tilde{r}_D^{-}({x_{i}}) + \tilde{w}_{D}(x_{i}), \quad \tilde{r}^{+}_{D}(y)=\tilde{r}_D^{+}({x_{i+1}}) - \tilde{w}_{D}(x_{i+1}), \quad \tilde{w}_{D}(y)=0$

扩展后的函数仍然满足上面三个条件。

2.1.4 ε-approximate quantile summary

给定quantile suammary $Q(D) = (S, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$, 对于任意的$y \in R$，如果满足：

$$\tilde{r}^{+}_{D}(y) - \tilde{r}^{-}_{D}(y) - \tilde{w}_{D}(y) \le \varepsilon w(D)$$

则$Q(D)$ 为 ε-approximate quantile summary。

对于$Q(D) = (S, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$， 当且仅当下面两个条件满足时，其为ε-approximate quantile summary：

$$\tilde{r}^{+}_{D}(x_{i}) - \tilde{r}^{-}_{D}(x_{i}) - \tilde{w}_{D}(x_{i}) \le \varepsilon w(D)$$ $$\tilde{r}^{+}_{D}(x_{i+1}) - \tilde{r}^{-}_{D}(x_{i}) - \tilde{w}_{D}(x_{i+1}) - \tilde{w}_{D}(x_{i}) \le \varepsilon w(D)$$

对于上面第二个不等式，可以理解为：开区间$(x_{i}, x_{i+1})$ 中权重之和，由此可以与“分桶”相结合。

2.2 初始化

给定multi-set $D=\{(x_1, w_1), (x_2, w_2), \cdots (x_n, w_n)\}$，$Q(D) = (S, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$可以定义为：$S=\{x\|(x, w) \in D\}$， 且对于$x \in S$:

$$\tilde{r}^{+}_{D}(x)=r^{+}_{D}(x), \quad \tilde{r}^{-}_{D}(x)=r^{-}_{D}(x), \quad \tilde{w}_{D}(x)=w_{D}(x)$$

此时，$Q(D)$是0-approximate quantile summary.

2.2 merge

假定：

$$Q(D_1) = (S_{1}, \tilde{r}_{D_1}^{+},\tilde{r}^{-}_{D_1}, \tilde{w}_{D_1})$$ $$Q(D_2) = (S_{2}, \tilde{r}_{D_2}^{+},\tilde{r}^{-}_{D_2}, \tilde{w}_{D_2})$$

令$D=D_1 \cup D_2$， 合并后的quantile sumamry为： $Q(D) = (S, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$满足：

$$S=\{x_1, x_2, \cdots, x_k\}, \quad x_i \in S_1 \quad or \quad x_i \in S_2$$ $$\tilde{r}^{+}_{D}(x_{i}) = \tilde{r}^{+}_{D_1}(x_{i}) + \tilde{r}^{+}_{D_2}(x_{i})$$ $$\tilde{r}^{-}_{D}(x_{i}) = \tilde{r}^{-}_{D_1}(x_{i}) + \tilde{r}^{-}_{D_2}(x_{i})$$ $$\tilde{w}_{D}(x_{i}) = \tilde{w}_{D_1}(x_{i}) + \tilde{w}_{D_2}(x_{i})$$

如果$Q(D_1)$是$\varepsilon_1$-approximate quantile summary以及$Q(D_2)$是$\varepsilon_2$-approximate quantile summary， 则：$Q(D)$ 为 $max(\varepsilon_1, \varepsilon_2)$-approximate quantile summary。

2.3 prune

给定 $Q(D) = (S, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$， 其中: $S=\{x_1, x_2, \cdots, x_k\}, x_i \in \{x\|(x, w) \in D\}$，给定memory budget $b$， prune操作会返回一个新的quantile summary

$$(Q(D^{\prime}) = (S^{\prime}, \tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D})$$

其中，

1、 $S^{\prime}=\{x_{1}^{\prime}, x_{2}^{\prime}, \cdots, x_{b+1}^{\prime} \}$， 且：

$$x_{i}^{\prime} = g(Q, \frac{i-1}{b}w{D})$$

2、 $D^{\prime}$中的$\tilde{r}_{D}^{+},\tilde{r}^{-}_{D}, \tilde{w}_{D}$与原summary保持一致；

并且 $Q(D^{\prime})$是 $(\varepsilon + \frac{1}{b})$-approximate quantile summary。

---

Reference

1. XGBoost: A Scalable Tree Boosting System
2. XGBoost: A Scalable Tree Boosting System Supplementary Material
3. A Fast Algorithm for Approximate Quantiles in High Speed Data Streams
4. XGBoost解读(2)–近似分割算法
5. Space-Efficient Online Computation of Quantile Summaries

----EOF-----